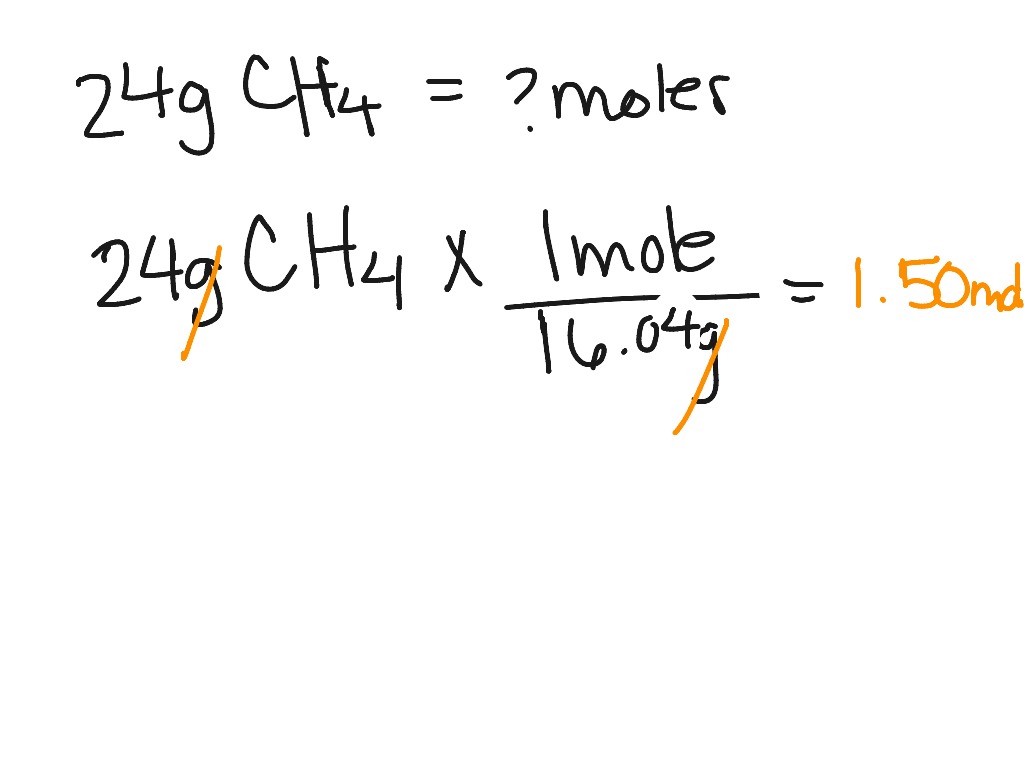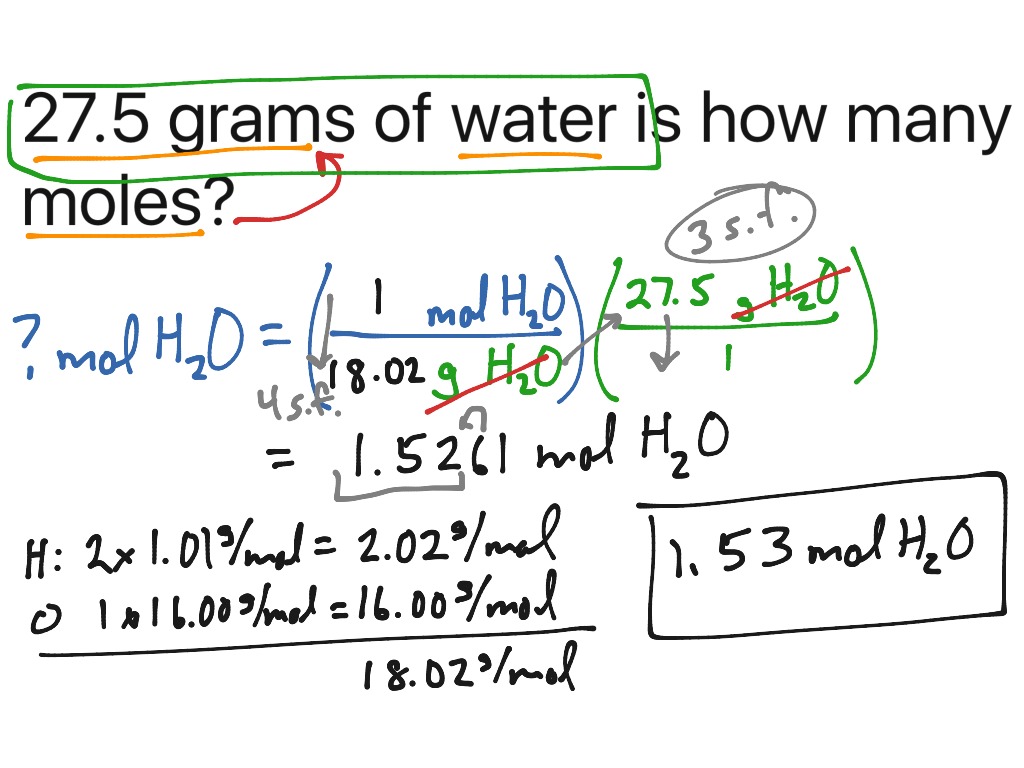The tube is bent into a "U" shape and mounted on an inexpensive piezoelectric speaker. The resonance frequency of the tube is detected by a photointerrupter, amplified, and fed into the speaker; the resulting feedback circuit keeps the glass tube vibrating at its resonance frequency. A peristaltic pump and computer are used to flow samples through the tube and record the resonance frequency of the tube. Detail of the glass tube shows the path followed by a sample inside the tube as it flows into the sensor ("a"), passes the tip of the sensor ("b"), and exits the sensor ("c"). Resonance frequency of the vibrating tube vs. time as a 770 μm diameter glass bead is passed back and forth through the tube eighteen times.
Each passage of the bead through the tube results in a momentary decrease in the tube's resonance frequency; this is recorded as a downward peak in the resonance frequency . Each point on the peak (baseline "a," tip "b," and baseline "c") corresponds with the bead's location in above. The height of this peak is used to determine the buoyant mass of the bead . Histograms showing the buoyant mass of another bead weighed thousands of times in two different fluid densities.
In deionized water (density 1.000 g/mL) the bead has an average buoyant mass of 3.69 ±0.12 μg, and in a sodium chloride solution (density 1.046 g/mL) the bead has an average buoyant mass of −4.42 ±0.16 μg. The widths of these distributions—120 and 160 nanograms—provide an estimate of the resolution of our mass measurements. Before using a vibrating tube to weigh a sample, the tube must first be calibrated.
We calibrated the sensor shown in Fig 1A using a glass bead of known size and density in a fluid of known density . Fig 1C shows eighteen downward peaks in the resonance frequency of the tube as the bead is pumped back and forth eighteen times through the tube. The height of each peak (72 millihertz; Fig 1D) is proportional to the buoyant mass of the bead .
Our homemade vibrating tube mass sensors typically have quality factors around 500, which is comparable to that of tuning forks and high enough for precise measurement of the tube's resonance frequency . When a sample passes through the vibrating tube sensor, its buoyant mass is recorded as a brief peak in the plot of resonance frequency vs. time (e.g., Fig 1C and 1D). Once a peak is located, the height of the peak can be measured and converted to a corresponding buoyant mass value using the sensor's point mass calibration described below.
Alternatively, a custom Python program can be used to fit the raw frequency measurements to an analytical equation of expected peak shape derived from Dohn et al. The resulting buoyant mass measurements were recorded and processed using a moving window average filter with a window size of five data points to slightly reduce noise in the plots of buoyant mass vs. time. Additional details about signal processing are provided in S6 Fig. In this work, we demonstrate a simple and inexpensive sensor capable of weighing microgram-sized objects in fluid. Like the SMR, this sensor uses a change in resonance frequency to weigh an object in fluid with high precision.
But unlike the SMR, this sensor can weigh samples with a large range of sizes and is extremely simple to fabricate. Our sensor consists of a short length of glass tubing bent into a "U" shape and attached to an inexpensive speaker that vibrates the glass tubing at its resonance frequency. The resulting sensor shown in Fig 1 costs about US $12 in materials and can be made in under 10 minutes.
Additionally, by weighing samples in fluids of different densities, we can also use our sensor to measure the volume and density of samples in fluid. The four proof-of-concept samples studied here—microbeads, embryos, seeds, and biomaterials—are representative of a wide range of samples that may be analyzed in fluid using vibrating glass tube sensors. Our technique is very versatile because all objects have fundamental physical properties like mass. Consequently, our mass sensor can be applied to problems as diverse as screening toxic substances, understanding the growth of plants, measuring the degradation of biomaterials, and many others. And unlike imaging-based measurements of size, our mass sensor is insensitive to the shape of the object. Finally, the automation, portability, and low cost of this technique make vibrating glass tubes particularly well suited for applications in the field or in resource-limited settings.
To determine the density of an irregular solid in pellet form, add approximately 40 mL of water to a clean and dry 100-mL graduated cylinder. Place the cylinder on an analytical balance and tare. Add approximately 10 pellets, and record the new volume after the addition. The mass is only the pellets, as the rest have been tared. Make at least two additional sets of mass and volume measurements to calculate an average value of the density. The density for zinc was measured for three different samples.
How To Find Mass Using Density And Volume Note that, since the measurements were made in a graduated cylinder, which is less precise than a volumetric flask, the density has lower degree of precision. Where mo is the absolute mass of the object, ρo is the density of the object, and ρf is the density of the fluid filling the channel. Stated in words, an object's buoyant mass is equal to its real mass minus the mass of an equivalent-volume amount of fluid.
If the object's density is less than the fluid's density, then the object has a negative buoyant mass and its passage through the tube will result in a momentary increase in the tube's resonance frequency . Finally, if the object's density equals the fluid's density, then the object will have zero buoyant mass and its passage through the tube will have no effect on the resonance frequency of the tube . Note that while the vibrating tube sensor is sensitive to an object's buoyant mass, it is not affected by buoyant forces because the object being measured is confined to the tube and cannot sink or float vertically. Thus, the orientation of the vibrating tube with respect to gravity has no effect on its measurements.
To simplify the comparison of densities of different materials across different units of measurement, other terms such as relative density or specific gravity are used. These dimensionless parameters represent the ratio of the mass density of a material to that of a standard material, typically water. Therefore, if the relative density of an object is less than one, that means that it is less dense than water and will likely float. Measurements of an object's fundamental physical properties like mass, volume, and density can offer valuable insights into the composition and state of the object. However, many important biological samples reside in a liquid environment where it is difficult to accurately measure their physical properties.
The density of a substance can be used to define the substance.Water is unusual because when water freezes, its solid form is less dense than liquid water, and thus floats on top of liquid water. Magnesium ribbon with a thickness of 250 μm (98% pure; MiniScience Inc., Clifton, NJ) was used as a model biomaterial in our degradation rate measurement studies. Roughly 1 mm sized pieces of magnesium were cut from the ribbon. The samples were polished before measurement using 600, 800, and 1200 grit silicon carbide abrasive papers to remove the native oxide layer.
Flow through the sensor was controlled using the servomotor as described previously. The resulting buoyant mass measurements are shown in Fig 4. To measure the density of a sample of material, both the mass and volume of the sample must be determined.
For both solids and liquids, a balance can be used to measure mass; however, methods for determining volume are different for solids and liquids. As liquids can flow and take the shapes of their containers, glassware such as a graduated cylinder or volumetric flask can be used to measure the volume of a liquid. The volume of an irregularly-shaped solid can be measured by submersion in a liquid — the difference in volume caused by addition of the solid is equal to the volume of the solid. Raw resonance frequency data from repeated measurements of a single polyethylene microbead in water (from the right-hand distribution of measurements in Fig 1E).
After zooming in to the filtered data , peaks corresponding to individual measurements of the microbead are visible. Zooming in further on one pair of peaks shows the ∼2 millihertz height of these peaks (corresponding to a buoyant mass of ∼3.7 μg for this microbead). The peaks come in pairs because the particular vibrating tube sensor used for this measurement had a tuning-fork shape with two vibrating "U"-shaped lobes . Volume is an amount of space, in three dimensions, that a sample of matter occupies.
The number and the phase of the molecules in the sample primarily determine the volume of a substance. Volume will be measured in many ways in this course, but the units are usually milliliters or cubic centimeters . Methods for determining or delivering precise volumes include volumetric pipets and pycnometers; less precise methods include burets, graduated cylinders, and graduated pipets. Table 1 lists results for the determination of the density of ethanol using a 50-mL volumetric flask. Densities were calculated by dividing the measured mass by 50.0 mL.
The mean measured density was 0.789 ± 0.001 g/mL. Table 2 lists results for the determination of the density of a sample of zinc metal using a 100-mL graduated cylinder and the liquid displacement method. Note that the measured densities are constant for both substances. Table 2, in particular, demonstrates that density is independent of the amount of substance studied. Finally, to demonstrate our technique using a biologically-relevant sample other than an organism, we used vibrating glass tubes to precisely measure the degradation rates of biodegradable materials.
For many applications in medical implants, it is desirable to have materials with known degradation rates. For example, a screw for repairing a broken bone might remain intact until the bone heals and then dissolve away. However, measuring the degradation rates of slow-degrading materials is a time-consuming and labor-intensive process. This process slows the development of new biomaterials and introduces the potential for human error.
To validate our technique with a diverse range of biological samples, we used vibrating tube sensors to monitor the mass of individual plant seeds during imbibition and germination. Seed imbibition, or water uptake, is used in agriculture as a metric of seed health and quality . Seed germination is a change in seed metabolism when imbibition starts; germination culminates with the elongation of the embryonic axis that penetrates the seed coating. The imbibition of seeds is accompanied by a rapid leakage of cellular materials and the rate of this leakage is decreased as the tissues become hydrated . If water uptake by the seed is too rapid, the seed tissue might experience injury, and if the seed enters an anaerobic state, the seed might experience accumulation of toxic chemicals such as ethanol. Both situations can encourage undesirable seed dormancy and delay germination .
In summary, seed imbibition and germination are important phenomena in plant research, and quantitative measurements of these phenomena would be valuable in a wide range of botanical and agricultural fields. As an object passes through the vibrating tube sensor, the shape of each resulting peak in the tube's resonance frequency is a function of the vibrational mode and amplitude of the tube. In this work, the tubes are vibrating at their primary vibrational mode, meaning that the amplitude of vibration is highest at the tip (the bottom of the glass "U") and lowest at the base (the top of the "U").
As the particle leaves the tube (point "c" in Fig 1B) the tube's vibrational amplitude in this region decreases again, so the resonance frequency of the tube returns to baseline (point "c" in Fig 1D). General mathematical expressions for predicting this peak shape for any vibrational mode were derived by Dohn et al. Ρ is the object's density m is the object's total mass V is the object's total volume Under specified conditions of temperature and pressure, the density of a fluid is defined as described above. However, the density of a solid material can be defined in several ways. Porous or granular materials have a density of the solid material, as well as a bulk density, which can be variable.
For example, if you gently fill a container with sand, and divide the mass of sand by the container volume you get a value termed loose bulk density. If you took this same container and tapped on it repeatedly, allowing the sand to settle and pack together, and then calculate the results, you get a value termed tapped or packed bulk density. Tapped bulk density is always greater than or equal to loose bulk density. In both types of bulk density, some of the volume is taken up by the spaces between the grains of sand. The density of the sand grains, exclusive of the air between the grains, will be higher than the bulk density.
Of a substance is the ratio of the mass of a sample of the substance to its volume. The SI unit for density is the kilogram per cubic meter (kg/m3). For many situations, however, this as an inconvenient unit, and we often use grams per cubic centimeter (g/cm3) for the densities of solids and liquids, and grams per liter (g/L) for gases.
Although there are exceptions, most liquids and solids have densities that range from about 0.7 g/cm3 to 19 g/cm3 . Table \(\PageIndex\) shows the densities of some common substances. Most solid substances are irregularly shaped, which complicates volume determination. It is inaccurate, for example, to determine the volume of a powder by measuring its dimensions. Instead of directly measuring dimensions or using glassware like a volumetric flask, it is necessary to make use of a liquid displacement method to measure the volume of an irregularly shaped solid. A graduated cylinder containing a known volume of liquid is tared.
The solid is added to the cylinder, and the total mass is weighed again to determine the mass of the solid. Addition of the solid causes an upward displacement of the liquid, resulting in a new volume reading. The volume of the solid is equal to the change in volume due to liquid displacement (i.e., the difference in liquid volume before and after adding solid). Additional measurements of the buoyant mass of single zebrafish embryos in water, obtained using our vibrating glass tube sensor.
In Fig 1C a slight downward drift is visible in the baseline resonance frequency of the vibrating tube over time; the frequency is decreasing at about 2 millihertz per minute. Slow baseline frequency drift like this is common in vibrating mass sensors and is mostly due to small fluctuations in the temperature of the sensor. However, the magnitude of this drift is small compared to the duration of a peak, which is why the baseline of an individual peak in Fig 1D is relatively flat.
Mass is one of the fundamental properties of an object in Physics, and is a measurement of how much matter there is in something. Matter is any substance that you can touch — anything that takes up physical space and has volume. Often, mass is related to size, but this isn't a perfect relationship, as objects like a large hot-air balloon often have less mass than a small boulder. To calculate mass, you'll first need the density and volume of the object.
Read on for details of the formula and to learn about different types of mass across scientific disciplines. The most accurate way to calculate the density of any solid, liquid or gas is to divide its mass in kilograms by its volume (length × width × height) in cubic metres. The density of water is approximately 1000 kg/m 3 and the density of air is approximately 1.2 kg/m 3.
To begin this procedure, place a clean and dry 50-mL volumetric flask on an analytical balance. After the measurement has stabilized, tare the balance. Use a funnel to add approximately 45 mL of liquid to the flask.